
Vocabulary
• Focal Length: The distance between a curved mirror and its Focal Point
• Focal Point: The position where all reflected light inside the telescope focuses to a point of light
• Focal Surface: The place where the Focal Point converges to
• Primary Mirror: The larger of the two curved mirrors that reflect the incoming light to the Secondary Mirror
• Secondary Mirror: The smaller of the two curved mirrors that direct reflected light from the Primary Mirror to the Focal Surface
Narrative
The Hubble Space Telescope (HST) is celebrating its 25th year in space. Launched in 1990, the HST fit snugly within the confines of the Space Shuttle’s Payload Bay, which had a length of 18 meters, or almost 60 feet. The HST overcame its initial flaws and went on to become a historic telescope, thanks to the intrepid high–flying Shuttle repair crews and the folks on the ground. Indeed, after the fixes, the effective Focal Length of the HST lived up to its design of a whopping 57.6 meters (189 feet)!
Wait. The Space Shuttle Payload Bay was 18 m long, and the HST has a focal length of almost 58 m long. That’s greater than the entire length of the Shuttle itself at 37 m (122 ft)! So how did the HST fit inside the Space Shuttle?
Enter the Cassegrain Telescope, a design that allows for a magnification factor! The HST is a Ritchey–Chrétien variant, which uses hyperbolic mirrors. A hole in the center of the Primary Mirror (M1)allows the reflected light from the smaller Secondary Mirror (M2)to pass through to the Focal Surface (F) located behind the Primary Mirror.
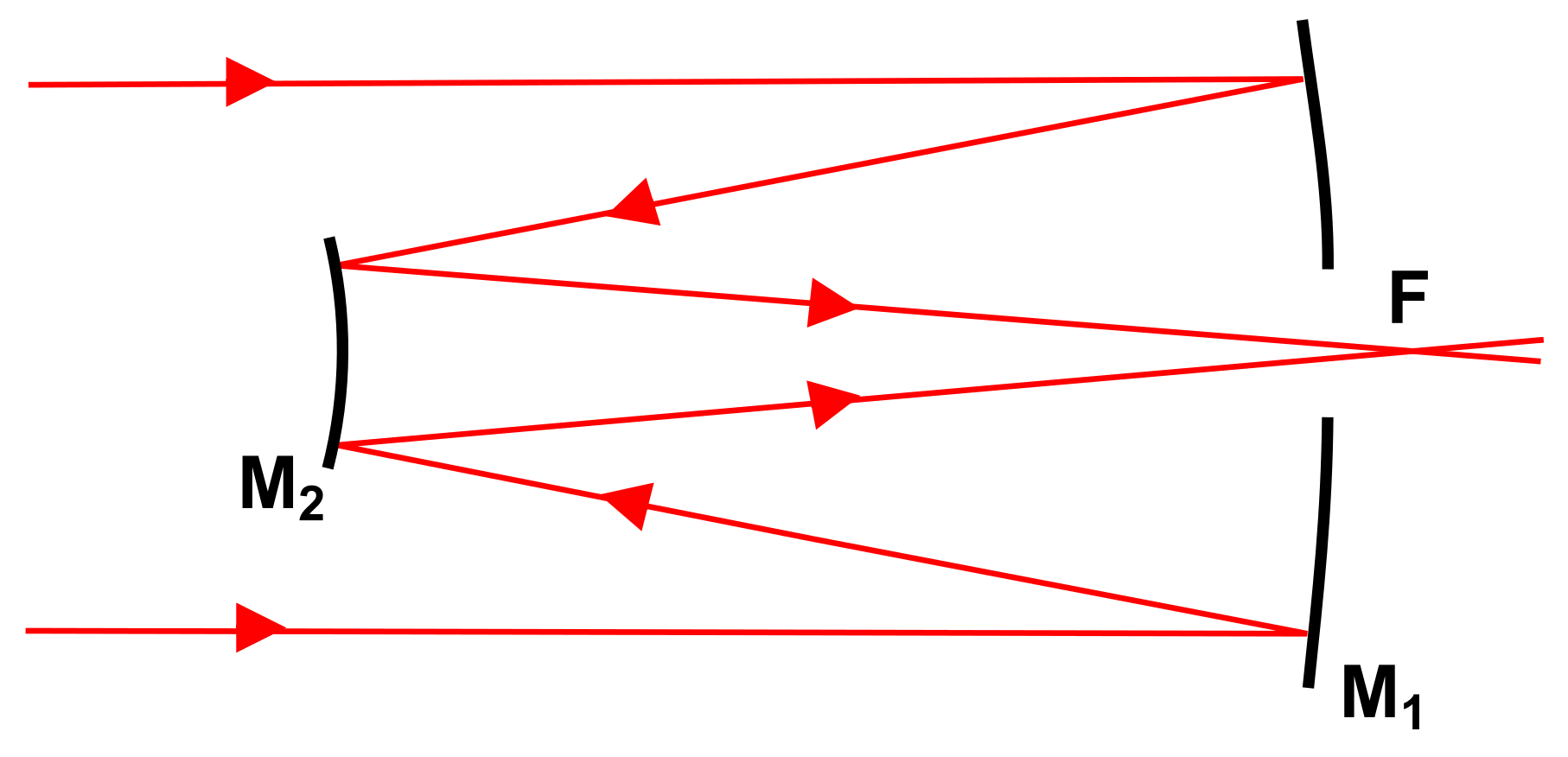
By extending the lines made from the reflected light bouncing off of M2 backwards,we can see how this magnification effect works:
The M2 mirror simply shortens the time needed to get to position F, the Focal Surface. The Effective Focal Length of a Cassegrain telescope (eFt) is:
eFt = Fp * q / p where,
Fp = Primary Mirror (M1)Focal Length
p = the system Focal Point (F) to Secondary Mirror (M2) distance
q = the M2 surface to the focal point of the M1mirror distance
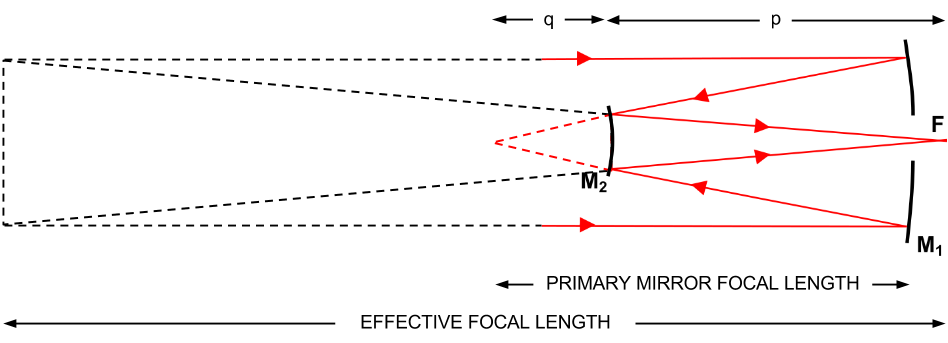
So let’s check those Effective Focal Length figures, shall we?
Example
Looking up the specifications of the HST, we find that the Focal Length of the Primary Mirror (Fp) is 5.52 m, the mirrors are separated by a distance (Md) of 4.91 m, and the Focal Surface (F) is 1.5 m behind the Primary Mirror.
So,
q = Md + F
= 4.91 + 1.5 = 6.41 m
p = Fp – Md
= 5.52 – 4.91 = 0.61 m
Therefore,
eFt = Fp * q / p
= (5.52) (6.41) / (0.61) = 58.0 m
Conclusion
Our calculation of 58.0 m is very close to the published figure of 57.6 m. This means that we can indeed fit a telescope with a large Focal Length inside a smaller cylindrical length. Sometimes great things really do come in small packages!
This also means that the HST magnifies the Primary Mirror Focal Length by a factor of ten. Holy Hubble Constant, Batman! No wonder it can see so far.
Despite its rough start, the HST has certainly earned its place in history, not only through the efforts of teams of people acting as one to give us mind–altering images of the Universe, but also by the use of clever mirror reflection techniques that allowed us to reach back even further in time and space.
Happy 25th Anniversary, Hubble Space Telescope!
For a more in-depth treatment of this high school project by Joe Maness & Rich Holtzin visit www.stemfortheclassroom.org.



